
Tras un año de búsquedas infructuosas, un equipo de estadísticos calculó el lugar del siniestro en apenas una semana
"A primera hora de la mañana del 1 de junio de 2009 el vuelo de Air France AF 447, con 228 personas a bordo, entre pasajeros y tripulación, desapareció en medio de una tormenta sobre el Atlántico en un vuelo desde Rio de Janeiro a París". Así empiezan describiendo el científico Lawrence Stone y sus colegas de Metron Scientific Solutions su papel en el descubrimiento de los restos del avión casi dos años después de la desaparición del aparato.
Stone y su equipo son estadísticos a los que se llamó para reexaminar las pruebas después de que cuatro búsquedas intensivas fueran incapaces de dar con el avión. Lo interesante de esta historia es que su análisis señaló una localización no demasiado alejada de la última posición conocida del avión, en un área en la que se ya había buscado después del desastre. Los restos se encontraron casi exactamente donde predijeron, a una profundidad de 4.200 metros, tras de una semana más de búsqueda.
Ahora los investigadores explican cómo lo hicieron. Su enfoque fue aplicar una técnica conocida como inferencia bayesiana que tiene en cuenta toda la información conocida sobre la localización del accidente, así como las pruebas derivadas de los esfuerzos de búsqueda infructuosos. El resultado es una distribución de probabilidad para la localización de los restos.
La inferencia bayesiana es una técnica estadística que los matemáticos usan para establecer la distribución de probabilidades subyacente basándose en una distribución observada. En concreto, los estadísticos aplican la técnica para actualizar la probabilidad de una hipótesis concreta mientras se recogen pruebas adicionales.
En el caso del vuelo de Air France AF 447, la distribución subyacente era la probabilidad de encontrar los restos en una localización dada. Algo que dependía de toda una serie de factores, como la última localización GPS transmitida por el avión, cómo de lejos pudo haber volado la aeronave después de eso, y también la localización de los cadáveres hallados en la superficie teniendo en cuenta el desplazamiento por las corrientes.
Todo esto es lo que los estadísticos denominan el "previo". Da una distribución de probabilidad para la localización del accidente.
Sin embargo, varias búsquedas que también confiaron en esta información no lograron encontrar los restos. Así que la pregunta a la que Stone y su equipo tenían que contestar era cómo usar estas pruebas para modificar la distribución de probabilidad.
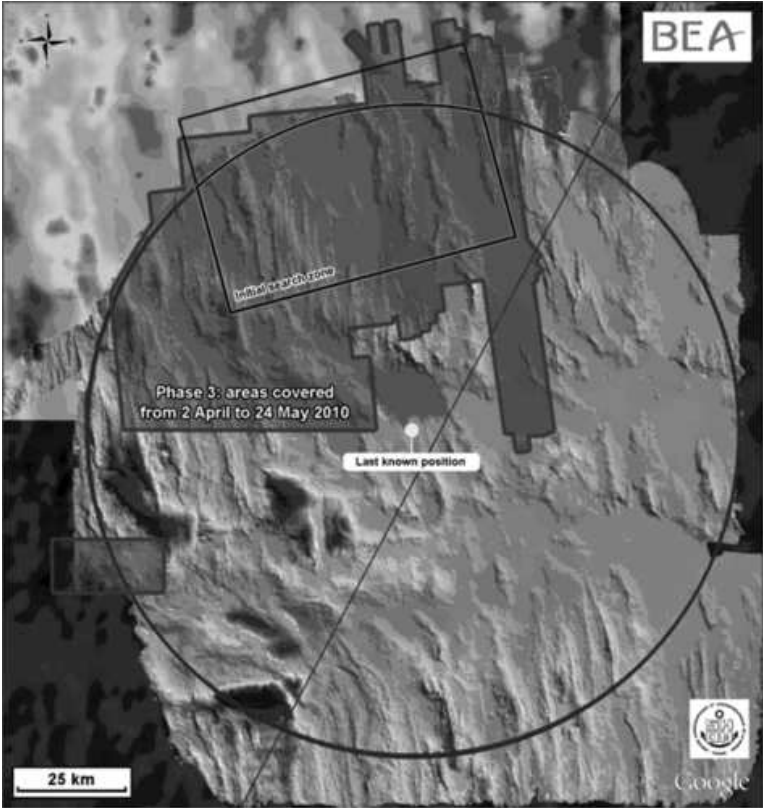
Esto es lo que los estadísticos denominan distribución posterior. Para calcularla, el equipo tuvo en cuenta el fracaso de cuatro búsquedas distintas después de que el avión cayera. El primer fracaso fue no encontrar ni restos ni cadáveres hasta seis días después de que el avión desapareciera en junio de 2009. Después estaba el fracaso de las búsquedas acústicas en julio de 2009 para detectar los pings de las balizas submarinas de la grabación de los datos del vuelo y del sonido de la cabina. Una búsqueda posterior en agosto de 2009 no consiguió encontrar nada usando sónar batimétrico y por último hubo otra búsqueda infructuosa usando sónar batimétrico en abril y mayo de 2010.
Todas las búsquedas tuvieron lugar en zonas distintas, a veces solapadas, en las 40 millas náuticas a la redonda de la última localización conocida del avión. Estas zonas se calcularon basándose en la distancia que podrían haber recorrido los restos y los cadáveres por efecto del viento y las corrientes. Y la búsqueda para detectar los pings acústicos de los grabadores de datos de la nave ya habían cubierto la zona donde finalmente se encontraron los restos.
Esta es una cuestión importante. Un análisis distinto podría haber excluido esta localización sobre la base de que ya se había registrado. Pero Stone y su equipo decidieron incluir la posibilidad de que las balizas acústicas hubieran fallado, una decisión clave que condujo directamente al descubrimiento de los restos. Sí que parece que las balizas fallaron y que este fue el motivo principal por el que la búsqueda llevó tanto tiempo.
Evidentemente, el punto a destacar es que la inferencia bayesiana no puede resolver estos problemas por sí misma. Quienes sí tienen un papel clave a la hora de evaluar las pruebas, decidir qué significan y después incorporarlas de forma adecuada al modelo bayesiano, son los estadísticos.
El resultado final, al menos en este caso, fue el descubrimiento de los restos junto con las grabaciones sobre los datos del vuelo y el del sonido de la cabina que proporcionaron pruebas fundamentales sobre los últimos instantes del vuelo (aunque aún se debate exactamente qué causó el desastre). También llevó al descubrimiento de muchos más cuerpos que pudieron entregarse a las familias.
Esta historia de la búsqueda mediante la estadística de un avión desaparecido es tremendamente relevante ahora que se busca el vuelo de Malaysia Airlines MH 370, que desapareció entre Kuala Lumpur y Pekín el 8 de marzo. No se ha vuelto a saber nada de él.
La lección aprendida de la búsqueda del vuelo AF 447 de Air France es que la inferencia bayesiana es una potente herramienta para búsquedas de este tipo, pero cómo se aplica es igual de importante. En otras palabras, los estadísticos también tendrán un papel relevante en esta búsqueda.
Esperemos que las suposiciones usadas para actualizar futuras búsquedas del MH 370 acaben teniendo tanto éxito como las empleadas por Stone y compañía en 2011
Ref: arxiv.org/abs/1405.4720: Search for the Wreckage of Air France Flight AF 447


