La semana pasada, la comunidad de investigación en inteligencia artificial (IA) se reunió en Nueva Orleans (EE. UU.) para la Conferencia Internacional sobre Aprendizaje de Representaciones (ICLR, por sus siglas en inglés), una de sus conferencias anuales más importantes. Los más de 3.000 asistentes y 1.500 artículos enviados la convierten en uno de los foros más estratégicos para intercambiar nuevas ideas en este campo.

Este año, las charlas y los trabajos aceptados se centraron en su mayoría en abordar cuatro de los principales desafíos del aprendizaje profundo: imparcialidad, seguridad, generalización y causalidad. Si ha estado siguiendo las publicaciones de MIT Technology Review en español, tendrá una ligera idea sobre los tres primeros. Hemos explicado cómo los algoritmos de aprendizaje automático actuales están sesgados, son susceptibles a ataques antagónicos y son muy limitados a la hora de generalizar los patrones que encuentran en un conjunto de datos de entrenamiento para múltiples aplicaciones. Así que la comunidad de investigación está trabajando para que la tecnología sea lo suficientemente sofisticada para mitigar estas debilidades.

De lo que no se sabe demasiado es del último reto: la causalidad. El aprendizaje automático funciona muy bien para encontrar correlaciones en los datos, pero ¿podría acaso entender la causalidad ? Si lo consiguiera sería un gran avance: si los algoritmos pudieran ayudarnos a aclarar las causas y los efectos de diferentes fenómenos en algunos sistemas complejos, aumentarían nuestra comprensión del mundo y descubrirían herramientas más poderosas para actuar.

El pasado lunes, en una sala repleta, el aclamado de la unidad de investigación de IA en Facebook y en la Universidad de Nueva York (EE.UU.) Léon Bottou, presentó un nuevo marco sobre cómo podríamos conseguirlo.

Idea # 1

Foto: Muestras de un conjunto de datos de manuscritos MNIST. Créditos: Wikipedia

Comencemos con la primera gran idea de Bottou: una nueva forma de pensar sobre la causalidad. Digamos que queremos crear un sistema de visión artificial que aprenda a reconocer números escritos a mano. (Se trata de un clásico problema que utiliza el ampliamente disponible conjunto de datos "MNIST" de la imagen superior) Entrenaríamos una red neuronal con muchísimas imágenes escritas a mano, cada una etiquetada con el número que representa, y obtendríamos un sistema bastante decente a la hora de reconocer nuevos números.

Pero, ¿qué pasaría si el conjunto de datos de entrenamiento se modificara ligeramente de tal manera que cada uno de los números escritos a mano también fuera de un color (rojo o verde)? Por un momento, podríamos pensar que, en realidad, no sabemos si al programa le resulta más útil el color o la forma para identificar el dígito. La estrategia habitual consiste en etiquetar cada parte de los datos de entrenamiento con ambas características y dejar que la red neuronal decida.

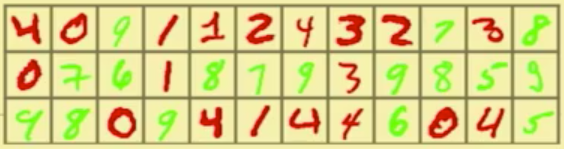
Foto: Muestras de un conjunto de datos MNIST en color. Créditos: Leon Bottou

Aquí es donde las cosas se ponen interesantes. El conjunto de datos "MNIST coloreado" es deliberadamente engañoso. En el mundo real, sabemos que el color de los datos es completamente irrelevante, pero en este conjunto de datos en particular, el color es, de hecho, un predictor más fuerte para el dígito que su forma. Así que nuestra red neuronal aprende a usar el color como predictor primario. Eso está bien si luego usamos la red para reconocer otros números escritos a mano que siguen los mismos patrones de colores. Pero el resultado fracasa completamente cuando se cambian los colores de los números. (Cuando Bottou realizó este experimento mental con datos de entrenamiento reales y una red neuronal real, logró un 84,3 % de precisión de reconocimiento en el primer escenario y solo un 10 % de precisión en el segundo).

En otras palabras, la red neuronal encontró lo que Bottou llama una "correlación falsa", lo que la hace completamente inútil fuera del limitadísimo contexto en el que se entrenó. En teoría, si pudiéramos deshacernos de todas las correlaciones falsas en un modelo de aprendizaje automático, solo nos quedarían las "invariables", aquellas que se mantienen verdaderas independientemente del contexto.

La invariabilidad permitiría comprender la causalidad, explica Bottou. Si conocemos las propiedades invariables de un sistema y sabemos la intervención realizada en un sistema, deberíamos poder deducir la consecuencia de esa intervención. Por ejemplo, si sabemos que la forma de un dígito manuscrito siempre dicta su significado, entonces se puede deducir que cambiando su forma (causa) cambiaría su significado (efecto). Otro ejemplo: si sabemos que todos los objetos están sujetos a la ley de la gravedad, podemos deducir que cuando soltamos una bola (causa), caerá al suelo (efecto).

Obviamente, estos son unos ejemplos muy simples de causa y efecto basados ​​en propiedades invariables que ya conocemos, la cuestión es, ¿cómo podríamos aplicar esta idea a sistemas mucho más complejos que aún no entendemos? ¿Qué pasaría si pudiéramos encontrar las propiedades invariables de nuestros sistemas económicos, por ejemplo, para poder entender los efectos de la implementación de la renta básica universal? ¿O las propiedades invariables del sistema climático de la Tierra, para poder evaluar el impacto de varias estrategias de geoingeniería?

Idea # 2

Entonces, ¿cómo nos deshacemos de estas correlaciones falsas? Esta es la segunda gran idea de Bottou. En la práctica actual de aprendizaje automático, la intuición predeterminada consiste en acumular datos tan diversos y representativos como sea posible en un solo conjunto de entrenamiento. Pero Bottou asegura que este enfoque resulta contraproducente. Los diferentes datos que provienen de diferentes contextos, ya sea porque se recopilan en diferentes momentos, en diferentes ubicaciones o en diferentes condiciones experimentales, deben conservarse como conjuntos separados y no mezclados y combinados. Cuando se consolidan, como ahora, la importante información contextual se pierde, lo que produce una probabilidad mucho mayor de correlaciones falsas.

Entrenar una red neuronal con múltiples conjuntos de datos específicos a sus contextos es un proceso muy diferente. La red ya no puede encontrar las correlaciones que solo son verdaderas solo en un único conjunto de datos de entrenamiento diverso; debe encontrar las correlaciones que son invariables en todos los conjuntos de datos diversos. Y si esos conjuntos se seleccionan de forma inteligente de un espectro completo de contextos, las correlaciones finales también deben coincidir estrechamente con las propiedades invariables de la verdad básica.

Así que, volviendo una vez más a nuestro ejemplo simple de MNIST de colores y basándose en esa teoría de encontrar propiedades invariables, Bottou volvió a realizar su experimento original. Esta vez usó dos conjuntos de datos MNIST de colores, cada uno con diferentes patrones de color. Luego entrenó su red neuronal a encontrar las correlaciones que se mantenían en ambos grupos. Cuando probó este modelo mejorado con nuevos números con los mismos patrones de color invertidos, logró una precisión de reconocimiento del 70 % para ambos. Los resultados demostraron que la red neuronal había aprendido a ignorar el color y a centrarse solo en las formas de los números.

Bottou resalta que su trabajo sobre estas ideas no está terminado, y la comunidad de investigación tardará bastante en probar las técnicas en problemas más complicados que los números de colores. Pero el marco sugiere el potencial del aprendizaje profundo para ayudarnos a comprender por qué suceden las cosas y, por lo tanto, darnos más control sobre nuestros destinos.