
Hasta ahora, la técnica para solucionar estas ecuaciones se basaba en la fórmula propuesta por los babilonios hace 4.000 años que, aunque útil, resulta muy complicada de ejecutar. Ahora, este investigador ha encontrado un método mucho más sencillo e intuitivo
Los antiguos babilonios eran impresionantes. Entre muchos de sus grandes logros, figura una solución matemática, ahora bien conocida, para un reto desagradable: el de pagar impuestos. Cualquier trabajador de la antigua Babilonia se enfrentaba a este problema: dada la factura de impuestos que se debe pagar en cultivos, ¿cuánto debería aumentar el tamaño de su campo para poder pagarla?
Este problema puede escribirse como una ecuación de segundo grado de la siguiente forma Ax 2 + Bx + C = 0. Y se resuelve con esta fórmula:
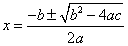
Ahora, más de 4.000 años después, millones de personas tienen esta ecuación de segundo grado grabada en la mente gracias a la forma en la que se enseñan las matemáticas en todo el planeta. Pero el número de personas capaces de resolverla es mucho menor, algo que también se debe a cómo se enseñan las matemáticas. La solución más común se basa en un truco matemático, llamado "completar el cuadrado", que no resulta nada intuitivo. De hecho, después de los babilonios, los matemáticos tardaron muchos siglos en descubrirlo.
Además, los matemáticos siempre encontraban muchas otras formas de resolver esa fórmula. Pero todas también resultaban muy difíciles y poco intuitivas. Así que resulta fácil imaginar que los matemáticos han intentado encontrar otra estrategia más sencilla de resolver las ecuaciones de segundo grado pero que, simplemente, no la han encontrado.
Esto acaba de cambiar gracias al trabajo del matemático de la Universidad Carnegie Mellon en Pittsburgh (EE. UU.) Po-Shen Loh. El investigador ha encontrado una forma más simple, que parece haber pasado desapercibida en estos 4.000 años.
El enfoque de Loh no se basa en completar el cuadrado ni en ningún otro truco matemático difícil. De hecho, es tan fácil que funciona como un método general en sí mismo, lo que significa que los estudiantes no necesitan recordar la fórmula en absoluto. "Esta solución tiene el potencial de desmitificar la fórmula cuadrática para los estudiantes de todo el mundo", afirma.
El nuevo enfoque es sencillo. Empieza con la observación de que si una ecuación de segundo grado se puede factorizar de la siguiente manera:
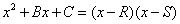
Entonces la parte derecha de la ecuación es igual a 0 cuando x = R o cuando x = S. Entonces esas serían las raíces de la ecuación de segundo grado. Multiplicar el lado derecho da el siguiente resultado:
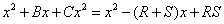
Esto se cumple cuando -B = R + S y cuando C = RS.
Ahora viene la parte ingeniosa. Loh señala que los números, R y S, se suman a -B cuando su media es -B / 2. El investigador detalla: "Así que buscamos dos números de la forma -B / 2 ± z, donde z es la única constante desconocida". Luego es posible multiplicar estos números para obtener una solución para C. Entonces:
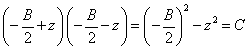
Después, un simple cambio de lugar da lo siguiente:
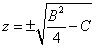
Eso significa que la solución para la ecuación de segundo grado es:
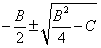
Voilà! Esa es la fórmula cuadrática.
[La versión más general se puede obtener al dividir la ecuación Ax 2 + Bx + C = 0 por A para llegar a: x 2 + B / Ax + C / A = 0 y luego repetir el proceso anterior.]
Se trata de una mejora muy significativa frente al método anterior, y Loh lo demuestra con un simple ejemplo. Encuentre las raíces de la siguiente ecuación de segundo grado: x 2 - 2x + 4 = 0
El método tradicional calcularía los valores para A, B y C y los pondría en la fórmula cuadrática. Pero el enfoque de Loh resuelve el problema intuitivamente. El primer paso consiste en pensar que las dos raíces de la ecuación deben ser iguales a -B / 2 ± z = 1 ± z
Y como su producto debe ser C = 4, podemos escribir:
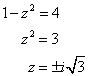
Entonces las raíces son:
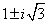
Intentar resolver el mismo problema mediante el método tradicional es mucho más complicado. ¡Venga, inténtelo! El nuevo enfoque es mucho más fácil y más intuitivo, sobre todo porque no requiere memorizar la fórmula en absoluto.
Una pregunta curiosa es por qué nadie ha encontrado ni compartido ampliamente este método antes. Loh sostiene que "en realidad estaría muy sorprendido si este enfoque no se hubiera descubierto hasta el día de hoy, dados los 4.000 años de historia sobre este tema, y los miles de millones de personas que han encontrado la fórmula y su solución. Sin embargo, esta técnica no es tan ampliamente enseñada o conocida".
Loh ha buscado un enfoque que se parezca al suyo en la historia de las matemáticas, pero no ha encontrado nada. Ha analizado los métodos desarrollados por los antiguos babilonios, chinos, griegos, indios y árabes, así como los de los matemáticos modernos del Renacimiento hasta hoy. Ninguno de ellos parece haber dado este paso, a pesar de que el álgebra es simple y se conoce desde hace siglos.
Entonces, ¿por qué ahora? Loh cree su hallazgo tiene que ver con cómo el enfoque tradicional demuestra que las ecuaciones de segundo grado tienen dos raíces. "Tal vez la razón es porque en realidad no es matemáticamente trivial hacer la implicación inversa: que siempre tiene dos raíces, y esas raíces suman -B más producto C", explica.
Loh, educador matemático y destacado divulgador, descubrió su enfoque al analizar los planes de estudio de matemáticas para los escolares, con el objetivo de desarrollar nuevas explicaciones. La solución surgió de este proceso.
La pregunta ahora cuánto se propagará y a qué velocidad. Para acelerar la adopción, Loh ha creado un vídeo sobre su método. Los gestores de impuestos de Babilonia seguramente habrían quedado impresionados.
Ref: arxiv.org/abs/1910.06709 : A Simple Proof of the Quadratic Formula

