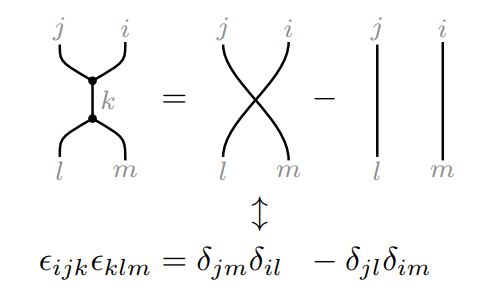
El científico revolucionó la física de partículas con sus representaciones gráficas. Ahora los matemáticos quieren hacer lo mismo para el cálculo vectorial, y parece que lo han conseguido
En 1948, la revista Physical Review publicó un artículo titulado Enfoque espacio-tiempo para la electrodinámica cuántica escrito por un joven físico llamado R.P. Feynman de la Universidad de Cornell (EE. UU.). El artículo describía una nueva forma de resolver los problemas de electrodinámica mediante matrices. No obstante, hoy es recordado por un descubrimiento mucho más importante: el diagrama de Feynman, que apareció impreso ahí por primera vez.
Los diagramas de Feynman han tenido un gran impacto en la física. Son representaciones pictóricas de las matemáticas que describen la interacción entre partículas subatómicas. En las matemáticas, cada interacción es una serie infinita, por lo que incluso las interacciones simples entre partículas son increíblemente complejas de describir de esta manera.
El genio de Feynman representó estas series con líneas simples en un formato gráfico, permitiendo a los científicos pensar en la física de partículas de una forma nueva y emocionante.
Feynman y otros inmediatamente empezaron a ampliar sus ideas usando esta abreviación gráfica. De hecho, el físico estadounidense Frank Wilcjek, que trabajó con Feynman en la década de 1980, escribió: "Los cálculos que finalmente me llevaron a ganar el Premio Nobel en 2004 hubieran sido literalmente impensables sin los diagramas de Feynman".
Por supuesto, muchas otras áreas de la física dependen de las matemáticas complejas. Y eso plantea la interesante pregunta de si las innovaciones basadas en gráficos podrían simplificar estos cálculos y quizás iniciar una nueva era de innovación, tal como lo hizo Feynman.
El investigador de la Universidad Nacional de Seúl en Corea del Sur Joon-Hwi Kim y un par de colegas suyos han ideado una innovación similar para el cálculo vectorial: una abreviación basada en gráficos para una de las herramientas matemáticas más comunes y poderosas en la ciencia. En su artículo afirman: "Creemos que el cálculo vectorial gráfico reducirá las barreras en el aprendizaje y en la práctica del cálculo vectorial, como hicieron los diagramas de Feynman en la teoría cuántica de campos".
Primero algunos antecedentes. El cálculo vectorial es una rama matemática que se ocupa de la diferenciación e integración de los campos vectoriales. La razón por la que es tan importante en física es que casi todo en el universo se puede describir en términos de campos vectoriales: campos electromagnéticos, campos gravitacionales, flujo de fluidos, etcétera.
Es por eso por lo que todo estudiante de física e ingeniería debe dedicar muchas horas a las matemáticas y notaciones crípticas necesarias. El problema es que los campos vectoriales son entidades complejas: asignan un solo vector a cada punto en el espacio tridimensional y pueden ser representaciones de objetos matemáticos más complejos llamados funciones diferenciables. Así que, en su forma más simple, un campo vectorial puede ser una lista infinita de vectores.
Los matemáticos representan estos campos usando un enfoque llamado notación indicial. Un vector puede escribirse como ai donde i = 1, 2 o 3 en un espacio tridimensional. Otra forma de escribir esto es: = [a 1, a 2, a 3].
Los problemas surgen cuando estas cantidades interactúan matemáticamente. Los campos vectoriales se pueden multiplicar por escalares o entre sí de dos maneras diferentes, conocidas como producto punto y producto cruz. Y los resultados pueden ser increíblemente complejos: como matrices enormes y multidimensionales.
En todos estos casos, los índices de los campos vectoriales involucrados deben ser seguidos con cuidado. Cualquier físico sabe lo fácil que es perder un índice y lo complicado que resulta encontrarlo de nuevo.
Luego está el desafío de determinar cómo cambian estos campos con el tiempo, o en relación con alguna otra variable. Este es el problema de la diferenciación, para el cual los físicos han desarrollado una serie de herramientas conocidas como operadores diferenciales, siendo quizás el más famoso el del operador o nabla.
El avance que han conseguido Kim y sus colegas consiste en el desarrollo de una notación basada en gráficos que sustituye la notación con índice. Representan un vector como un cuadro con una línea adjunta. En cambio, un escalar no tiene líneas que se extiendan desde él.
Cuando dos vectores se multiplican entre sí a través de un producto punto, el resultado es una cantidad escalar. La notación de Kim y su equipo se encarga de esto automáticamente. En un producto punto, las líneas asociadas con los dos vectores se conectan entre sí, creando un objeto sin líneas externas, en otras palabras, un escalar.
Pero un producto cruz entre dos vectores produce otro vector, y nuevamente la notación de Kim y su equipo lo maneja automáticamente. El gráfico para un producto cruz tiene forma de y, con las líneas de los dos vectores conectadas a una tercera que se extiende. En otras palabras, forma un vector.
Y es solo el comienzo. Los investigadores continúan describiendo una amplia gama de otras herramientas matemáticas, como el operador del junto con varias identidades importantes utilizadas en el cálculo vectorial. Y extienden sus ideas a los tensores, que son objetos matemáticos más complejos, cada uno con dos o más índices.
Los resultados ofrecen un ahorro considerable. Kim y sus compañeros muestran cómo su notación convierte las expresiones matemáticas complejas en gráficos relativamente simples, al igual que los diagramas de Feynman. "El lenguaje es altamente intuitivo y simplifica automáticamente las expresiones tensoriales", aseguran.
Hay una utilidad importante en su idea. Kim y su equipo sostienen que su enfoque transforma el cálculo del campo vectorial en una tarea visual, más bien como construir con Lego. El artículo detalla. "Como un niño que juega con juguetes educativos como los bloques de Lego o palos magnéticos de construcción, garabatear con estos diagramas será una experiencia entretenida. Como los diagramas de Feynman son el lenguaje más natural para describir el proceso microscópico de las partículas elementales, la notación gráfica es el lenguaje canónico del sistema de cálculo vectorial".
Es una gran afirmación con un enorme potencial. No hay duda de que los diagramas de Feynman han cambiado la forma en la que los físicos piensan sobre la física de partículas. Pero el cálculo vectorial tiene un alcance aún mayor como base matemática de gran parte de la física moderna e ingeniería.
La gran pregunta es lo ampliamente que se difundirán estas ideas. Eso determinará si esta notación gráfica desencadenará un cambio transformador en la forma en la que pensamos sobre la física o si formará una curiosa nota al pie de página en la historia de la invención matemática. En todo caso, Feynman seguramente se hubiera divertido con esto.
Ref: arxiv.org/abs/1911.00892: Boosting Vector Calculus with the Graphical Notation

