El científico informático Marijn Heule siempre busca un buen desafío matemático. Como profesor asociado de la Universidad Carnegie Mellon (EE. UU.), Heule tiene una reputación impresionante para resolver problemas matemáticos inabordables con herramientas computacionales. Su resultado de 2016 con el problema de los triples pitagóricos booleanos fue una tremenda demostración que acaparó los titulares: "La prueba matemática de doscientos terabytes es la más grande de todas". En la actualidad está implementando un enfoque automatizado para abordar la cautivadora y sencilla conjetura de Collatz.

Este problema de teoría de números propuesto por primera vez (según algunas fuentes) en la década de 1930 por el matemático alemán Lothar Collatz, ofrece una receta, o algoritmo, para generar una secuencia numérica. Se empieza con cualquier número entero positivo. Si el número es par, se divide por dos. Si el número es impar, se multiplica por tres y se le suma uno. Y luego se hace lo mismo, una y otra vez. La conjetura asegura que la secuencia siempre terminará en 1 (y luego continuamente pasará por 4, 2, 1).

El número 5, por ejemplo, lo cumple en solo seis pasos: 5, 16, 8, 4, 2, 1.

El número 27 recorre 111 cálculos, oscilando hacia arriba y hacia abajo, y su número más alto llega hasta 9.232, antes de acabar finalmente en el 1.

El número 40 genera otra breve secuencia: 40, 20, 10, 5, 16, 8, 4, 2, 1.

Hasta la fecha, la conjetura ha sido verificada por ordenador para todos los valores iniciales hasta casi 300.000 trillones, y cada número al final llega a 1.

La mayoría de los investigadores creen que la conjetura es cierta. Ha atraído a muchos matemáticos y no matemáticos por igual, pero nadie ha presentado una demostración. A principios de la década de 1980, el matemático húngaro Paul Erdős declaró: "Las matemáticas aún no están preparadas para tales problemas".

"Lo que queremos saber es si son mejores las personas o los ordenadores para resolver este tipo de problemas", Marijn Heule

"Y probablemente tenga razón", opina Heule. Para él, el atractivo de Collatz no es tanto la posibilidad de lograr un gran avance como el progreso de las técnicas de razonamiento automatizado. Después de estudiarlo durante cinco años, Heule y sus colaboradores, Scott Aaronson y Emre Yolcu, acaban de publicar un artículo en el servidor de preprints arXiv. "Aunque no conseguimos demostrar la conjetura de Collatz", escriben, "creemos que estas ideas representan un nuevo enfoque interesante".

"Es un noble fracaso", afirma el científico informático de la Universidad de Texas en Austin (EE. UU.) Scott Aaronson. Un fracaso porque no demostraron la conjetura. Noble porque progresaron en otro sentido: Heule lo ve como un punto de partida para determinar si son mejores las personas o los ordenadores para demostrar tales problemas.

Traducir matemáticas a computación

Para muchos problemas matemáticos, los ordenadores son inútiles, ya que no tienen acceso al vasto corpus matemático acumulado a lo largo de la historia. Pero a veces los ordenadores sobresalen donde las personas están desesperadas. Si a un ordenador se le dice cómo es una solución y se le asigna un objetivo y un espacio de búsqueda bien definido, podría encontrar esta con la fuerza bruta. Sin embargo, es un tema de debate si los resultados computacionales equivalen a adiciones significativas al canon matemático; la opinión tradicional es que solo la creatividad y la intuición humanas, a través de conceptos e ideas, amplían el alcance de las matemáticas, mientras que los avances a través de la informática a menudo se descartan como ingeniería.

En cierto sentido, el ordenador y la conjetura de Collatz son una combinación perfecta. Por un lado, como señala el especialista en lógica y profesor de filosofía de la Universidad de Carnegie Mellon Jeremy Avigad, la noción de un algoritmo iterativo está en la base de la informática, y las secuencias de Collatz son un ejemplo de un algoritmo iterativo, procediendo paso a paso de acuerdo con una regla determinada. De manera similar, mostrar que un proceso termina es un problema común en la informática. "Los informáticos generalmente quieren saber que sus algoritmos terminan, es decir, que siempre devuelven una respuesta", resalta Avigad. Heule y sus colaboradores están aprovechando esa tecnología para abordar la conjetura de Collatz, que en realidad es solo un problema de terminación.

"Lo bonito de este método automatizado es que uno puede encender el ordenador y esperar", Jeffrey Lagarias

Heule ha trabajado con una herramienta computacional denominada solucionador de SAT, o de satisfacibilidad, un programa informático que determina si existe una solución para una fórmula o para un problema con un conjunto de obstáculos. Lo que es crucial, en el caso de un desafío matemático, es que el solucionador de SAT primero necesita el problema traducido, o representado, en términos que el ordenador pueda entender. Y como subraya Yolcu, estudiante de doctorado de Heule: "La representación importa y mucho".

Una apuesta arriesgada, pero vale la pena intentarlo

Cuando Heule mencionó por primera vez abordar a Collatz con un solucionador de SAT, Aaronson pensó: "No hay manera de que esto funcione". Pero acabó convencido fácilmente de que valía la pena intentarlo, ya que Heule detectó algunas formas sutiles de transformar este viejo problema en más flexible. Se había dado cuenta de que una comunidad de científicos informáticos utilizaba los solucionadores SAT para encontrar con éxito pruebas de terminación para una representación abstracta de la computación denominada "sistema de reescritura".

Era una posibilidad remota, pero Heule sugirió a Aaronson que transformar la conjetura de Collatz en un sistema de reescritura podría hacer posible obtener una prueba de terminación para Collatz (Aaronson había ayudado previamente a transformar la hipótesis de Riemann en un sistema computacional, codificándola en una pequeña máquina de Turing). Esa misma noche, Aaronson diseñó el sistema. "Fue como hacer unos deberes, un ejercicio divertido", afirma.

"En un sentido muy literal, me enfrentaba a un Terminator, al menos a un demostrador de teoremas de terminación", Scott Aaronson

El sistema de Aaronson capturó el problema de Collatz con 11 reglas. Si los investigadores pudieran obtener una prueba de terminación para este sistema análogo, aplicando esas 11 reglas en cualquier orden, eso demostraría que la conjetura de Collatz es cierta.

Heule lo probó con las herramientas de última generación para demostrar la terminación de los sistemas de reescritura, pero eso no funcionó; fue decepcionante y sorprendente. "Estas herramientas están optimizadas para los problemas que se pueden resolver en un minuto, mientras que cualquier método para el de Collatz probablemente requiera días, o años, de computación", asegura Heule. Esto les motivó a perfeccionar su enfoque e implementar sus propias herramientas para transformar el problema de reescritura en un problema de SAT.

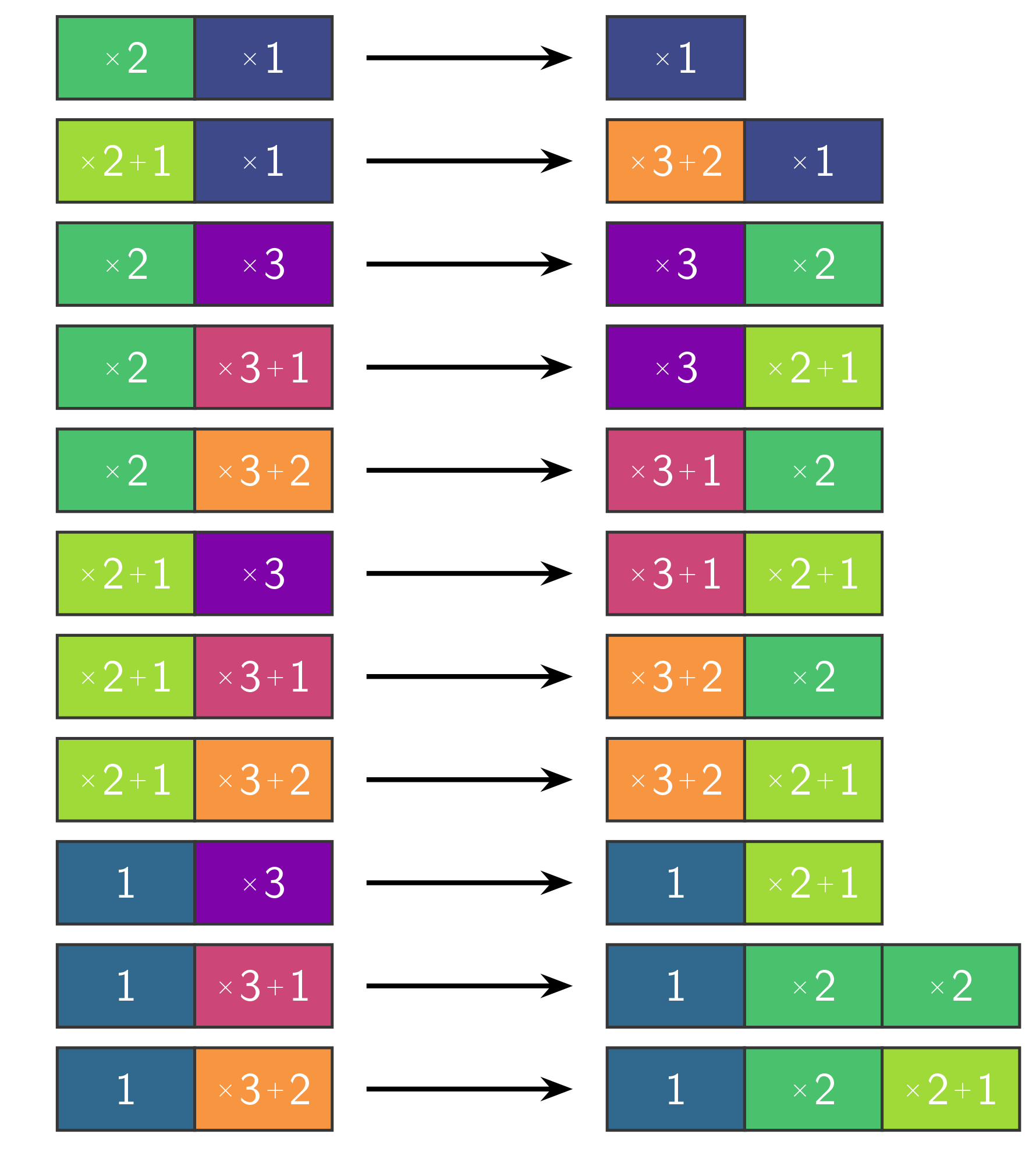
Foto: Una representación del sistema de reescritura de 11 reglas para la conjetura de Collatz. Créditos: Marijn Heule

Aaronson pensó que sería mucho más fácil resolver el sistema de las 11 reglas con una menos, creando así un sistema "similar al de Collatz", una prueba definitiva para el objetivo más amplio. Lanzó un desafío de personas contra los ordenadores: el primero en resolver todos los subsistemas con 10 reglas ganaba. Aaronson lo intentó a mano. Heule lo ha probado con el solucionador SAT: codificó el sistema como un problema de satisfacibilidad, con otra capa inteligente de representación, traduciendo el sistema a la jerga de las variables del ordenador que pueden ser 0 y 1, y luego dejó que su solucionador SAT se ejecutara en los núcleos, buscando prueba de la terminación.

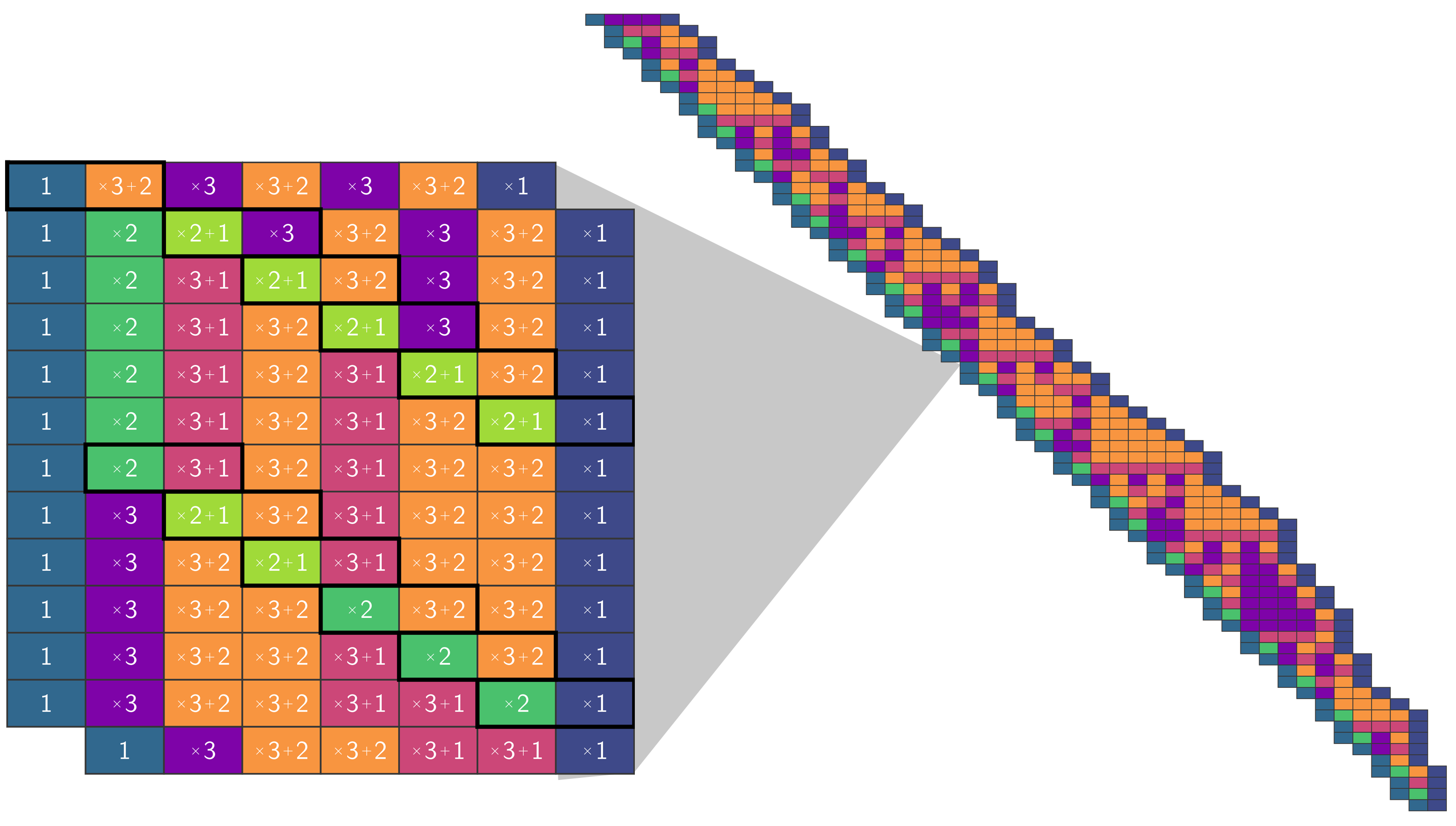
Foto: El sistema sigue la secuencia de Collatz para el valor inicial 27 (27 está en la parte superior izquierda de la cascada diagonal, 1 está en la parte inferior derecha). Hay 71 pasos, en vez de 111, ya que los investigadores utilizaron una versión diferente pero equivalente al algoritmo de Collatz: si el número es par, se divide por 2; de lo contrario, se multiplica por 3, se le suma 1 y luego se divide el resultado por 2. Créditos: Marijn Heule

Ambos lograron demostrar que el sistema termina con los diversos conjuntos de las 10 reglas. A veces era bastante simple, tanto para el ser humano como para el programa. El enfoque automático de Heule tardó como máximo 24 horas. El enfoque de Aaronson requirió un gran esfuerzo intelectual, y tardó varias horas o incluso un día (un conjunto de 10 reglas que nunca logró demostrar, aunque cree firmemente que podría hacerlo con más esfuerzo).  Aaronson dice: "En un sentido muy literal, me enfrentaba a un Terminator, al menos a un demostrador de teoremas de terminación".

Desde entonces, Yolcu ha perfeccionado el solucionador SAT, calibrando la herramienta para que se adapte mejor a la naturaleza del problema de Collatz. Estos trucos marcaron la diferencia: aceleraron las pruebas de terminación para los subsistemas de 10 reglas y redujeron los tiempos de ejecución a unos pocos segundos.

"La pregunta principal que queda", explica Aaronson, "sería: ¿qué pasa con el conjunto completo de 11 reglas? Si intentamos ejecutar el sistema en el conjunto completo simplemente no termina nunca, lo que tal vez no debería sorprendernos, porque así es el problema de Collatz".

Heule cree que la mayoría de las investigaciones sobre el razonamiento automatizado hace la vista gorda ante los problemas que requieren muchos cálculos. Pero basándose en sus avances anteriores, considera que estos problemas se pueden resolver. Otros han transformado el problema de Collatz en un sistema de reescritura, pero es la estrategia de manejar un solucionador SAT ajustado a escala con una potencia de cálculo formidable la que podría ganar tracción hacia la demostración.

Hasta ahora, Heule ha llevado a cabo la investigación de Collatz utilizando alrededor de 5.000 núcleos (las unidades de procesamiento que alimentan los ordenadores; los ordenadores de consumo tienen cuatro u ocho núcleos). Como becario de Amazon, tiene una invitación abierta de Amazon Web Services para acceder a los recursos "prácticamente ilimitados", hasta un millón de núcleos. Pero Heule es reacio a usar mucho más. Resalta: "Quiero alguna señal de que este es un intento realista". De lo contrario, cree que estaría desperdiciando recursos y confianza. "No necesito un 100 % de garantía, pero la verdad es que me gustaría tener alguna evidencia de que hay una probabilidad razonable de que tenga éxito".

Sobrealimentar una transformación

"Lo bonito de este método automatizado es que uno puede encender el ordenador y esperar", destaca el matemático de la Universidad de Michigan (EE. UU.) Jeffrey Lagarias. Ha jugado con Collatz durante unos cincuenta años y se ha convertido en el guardián del conocimiento, compilando bibliografías con sus notas y editando un libro sobre el tema, The Ultimate Challenge. Para Lagarias, el enfoque automatizado le recordó a un artículo de 2013 del matemático de la Universidad de Princeton (EE. UU.) John Horton Conway, quien reflexionó que el problema de Collatz podría estar entre una clase esquiva de problemas que son verdaderos e "indecidibles", pero a la vez no demostrablemente indecidibles. Como señaló Conway, "incluso podría ser que la afirmación de que no son demostrables no es demostrable, y así sucesivamente".

"Si Conway tiene razón", opina Lagarias, "no habrá demostraciones, automatizadas o no, y nunca sabremos la respuesta".

La persona que posiblemente se ha acercado más que nadie es el matemático de la Universidad de California en Los Ángeles (EE. UU.) Terence Tao. En 2019, Tao demostró que la conjetura de Collatz es "casi" cierta para "casi" todos los números ("casi" se basa en dos definiciones técnicas diferentes).

Tao cree que una demostración humana de la conjetura sería matemáticamente más significativa (para entender el por qué) que una demostración informática. "Pero el hecho de que un gran problema sin resolver recaiga en un demostrador automático podría impulsar una transformación revolucionaria en la forma en la que los matemáticos utilizan la asistencia informática en su trabajo", asegura. "Con un problema tan insoluble como este, aceptaremos todos los conocimientos que podamos obtener".

No obstante, lo que realmente quieren Heule y sus colaboradores es un escenario en el cual, usando este enfoque, con este problema, el ordenador tenga éxito donde el ser humano falla, o viceversa. "En este punto, no sabemos si estas técnicas son mucho más fuertes de lo que las personas pueden hacer a mano o no, o si los seres humanos pueden hacer cosas que el ordenador no puede", concluye Heule. "Lo que queremos saber es si son mejores las personas o los ordenadores para resolver este tipo de problemas".

Con ese fin, veamos quién resuelve primero la conjetura de Collatz.